openSCAD cos  函数

C 语言函数的描述：

#include
#include
#define PI 3.14159265
int main ()
{
double param, result;
param = 60.0;
result = cos ( param * PI / 180.0 );
printf ("The cosine of %f degrees is %f.\n", param, result );
return 0;
}

y=cos(45);
cube(y);
translate([1.5,0,0])
color("khaki")
cube(0.707106781);

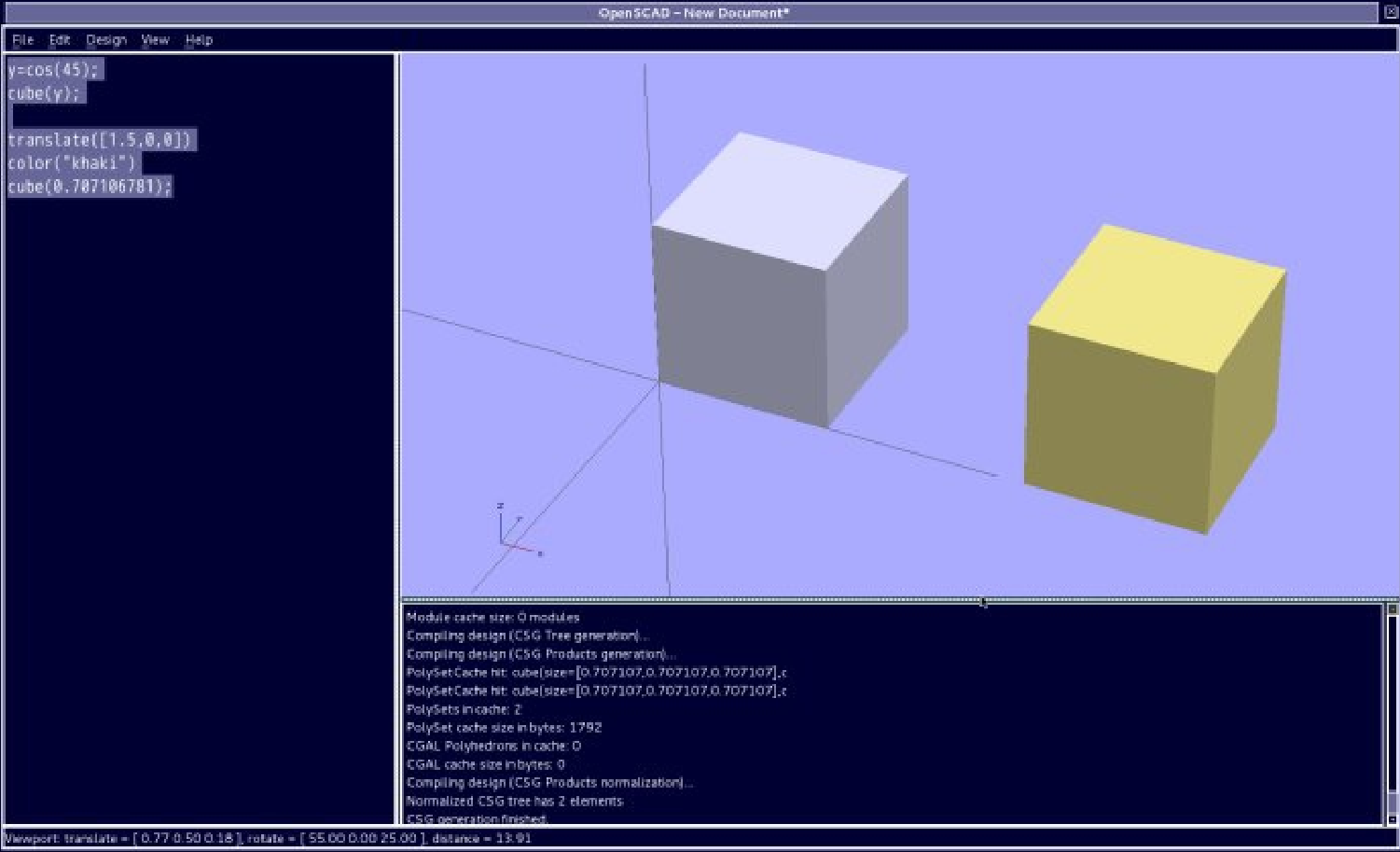
这里，更多的应用根据公式可以拓展。
公式： Cos (a) = x / r, 是根据已知 r 半径，或者循环增量 x 坐标 , 或者循环增量 a 角度，可以计算出一个圆弧轨迹。
实例：（这个实例是一个颜色分明的 12 小时时钟图形，用数学的的方法计算的 .)

r=150;
for(ag=[0:30:360])
{
if(ag==0)
{
color("blue")
translate([r,0,0])
sphere(r=15,$fn=100);
}
else{
if(ag>0 && ag<90)
{
color("pink")
translate([cos(ag)*r,sin(ag)*r,0])
sphere(r=5,$fn=100);
}
else{
if(ag==90)
{
color("green")
translate([0,r,0])
sphere(r=15,$fn=100);
}
else{
if(ag>90 && ag<180)
{
color("dodgerblue")
translate([cos(ag)*r,sin(ag)*r,0])
sphere(r=5,$fn=100);
}
else{
if(ag==180)
{
color("yellow")
translate([-r,0,0])
sphere(r=15,$fn=100);
}
else{
if(ag>180 && ag<270)
{
color("lawngreen")
translate([cos(ag)*r,sin(ag)*r,0])
sphere(r=5,$fn=100);
}
else{
if(ag==270)
{
color("red")
translate([0,-r,0])
sphere(r=15,$fn=100);
}
else{
if(ag>270 && ag<360)
{
color("peru")
translate([cos(ag)*r,sin(ag)*r,0])
sphere(r=5,$fn=100);
}
}}}}}}}
}

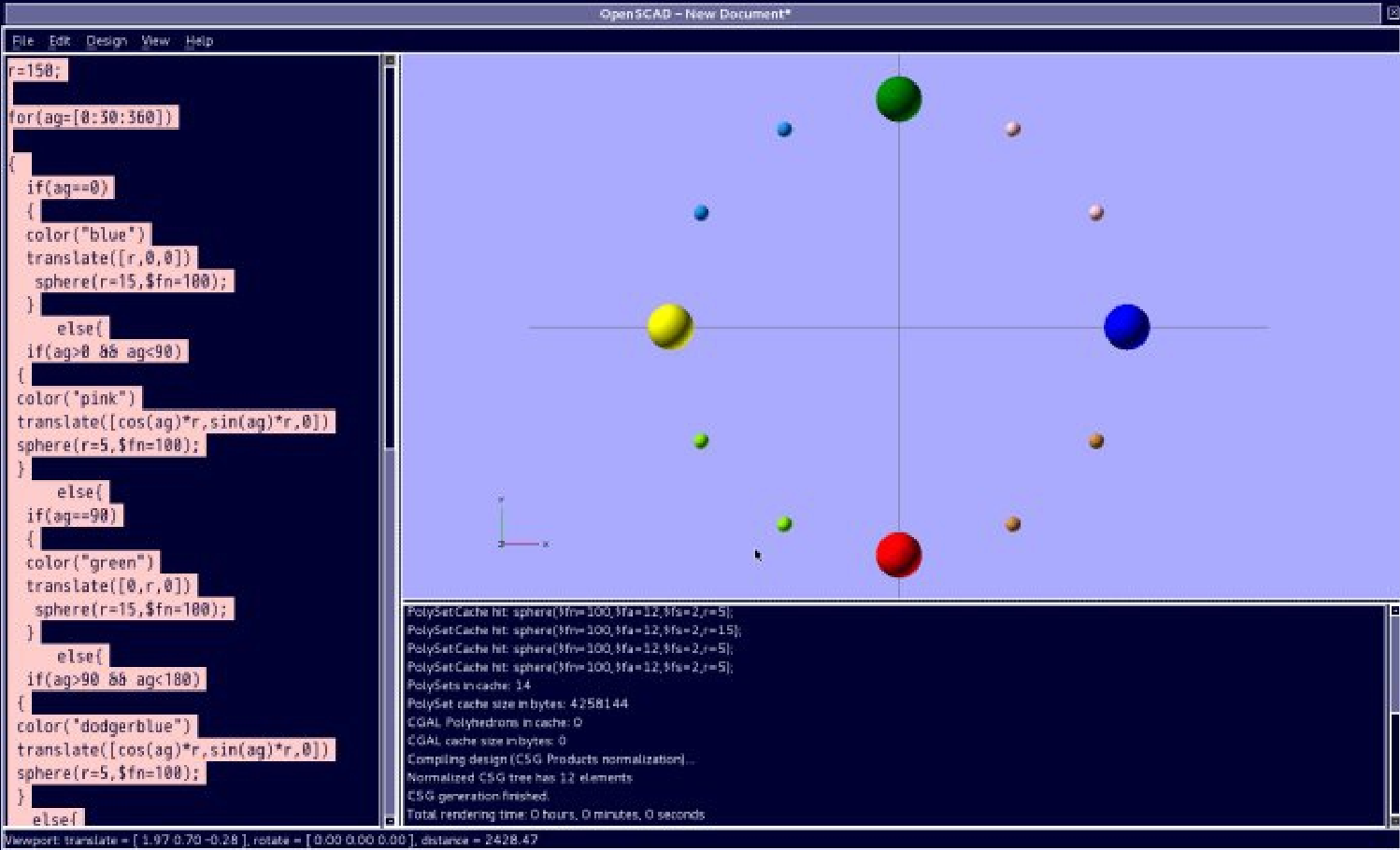
这里，还有一个相对简化的 12 位置时钟图形的画法：
实例代码：

r=150;
for(ag=[0:30:90])
{
if(ag>=0 && ag< 90)
{
color("red")
translate([cos(ag)*r,sin(ag)*r,0])
sphere(r=5,$fn=100);
}
if(ag>0 && ag<=90)
{
color("yellow")
translate([-cos(ag)*r,sin(ag)*r,0])
sphere(r=5,$fn=100);
}
if(ag>=0 && ag<90)
{
color("blue")
translate([-cos(ag)*r,-sin(ag)*r,0])
sphere(r=5,$fn=100);
}
if(ag>0 && ag<=90)
{
color("green")
translate([cos(ag)*r,-sin(ag)*r,0])
sphere(r=5,$fn=100);
}
}

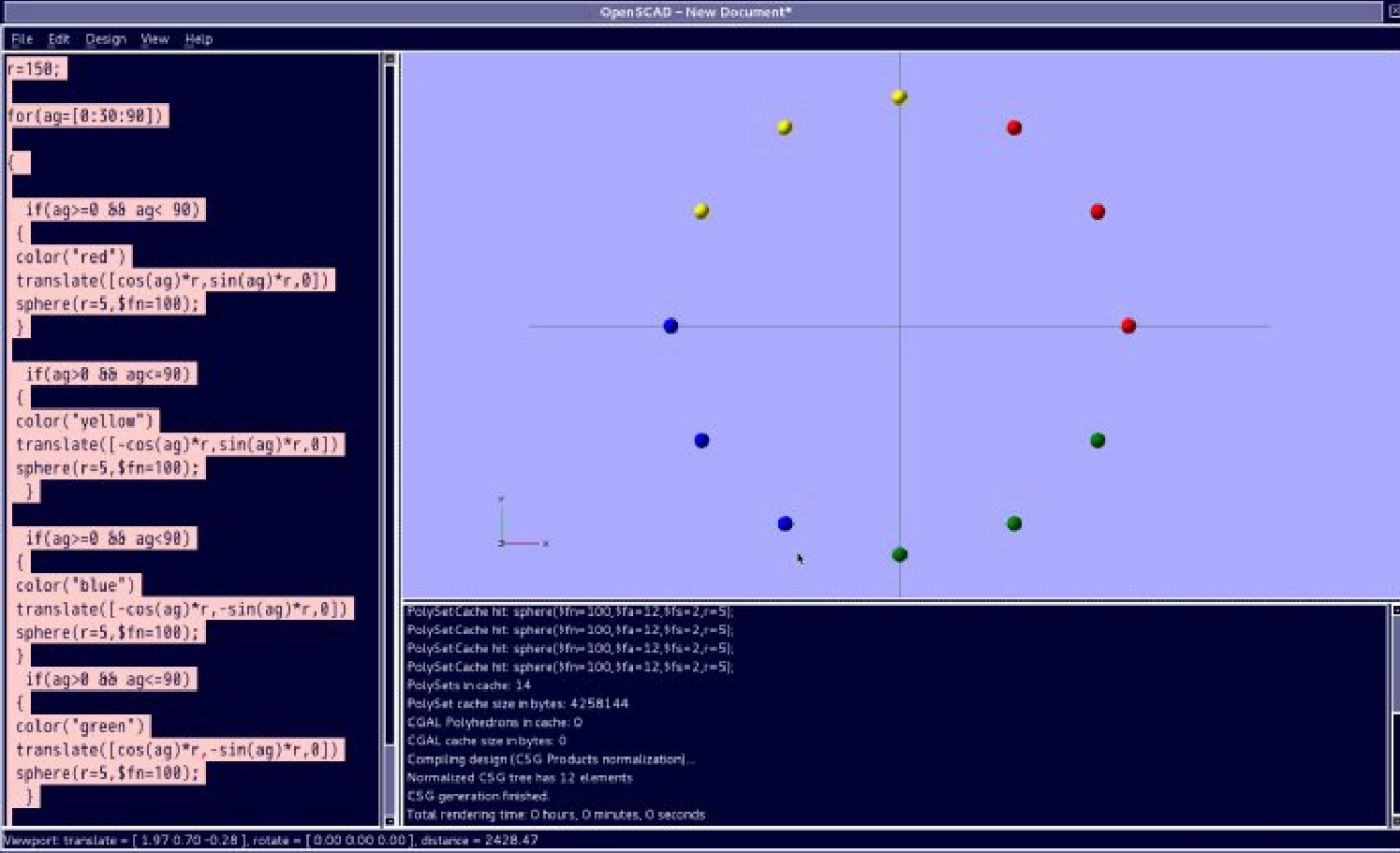
还有一个最简单的方法，上边的两个实例是使用了一些刚刚学习的数学运算符，逻辑运算符， 循环，条件选择，等等，更好的方便了学习 openSCAD 的各个功能。
更简单的 12 位置时钟图形的画法：
实例代码：

r=150;
for(ag=[0:30:360])
{
color("papayawhip")
translate([cos(ag)*r,sin(ag)*r,0])
sphere(r=10,$fn=100);
}

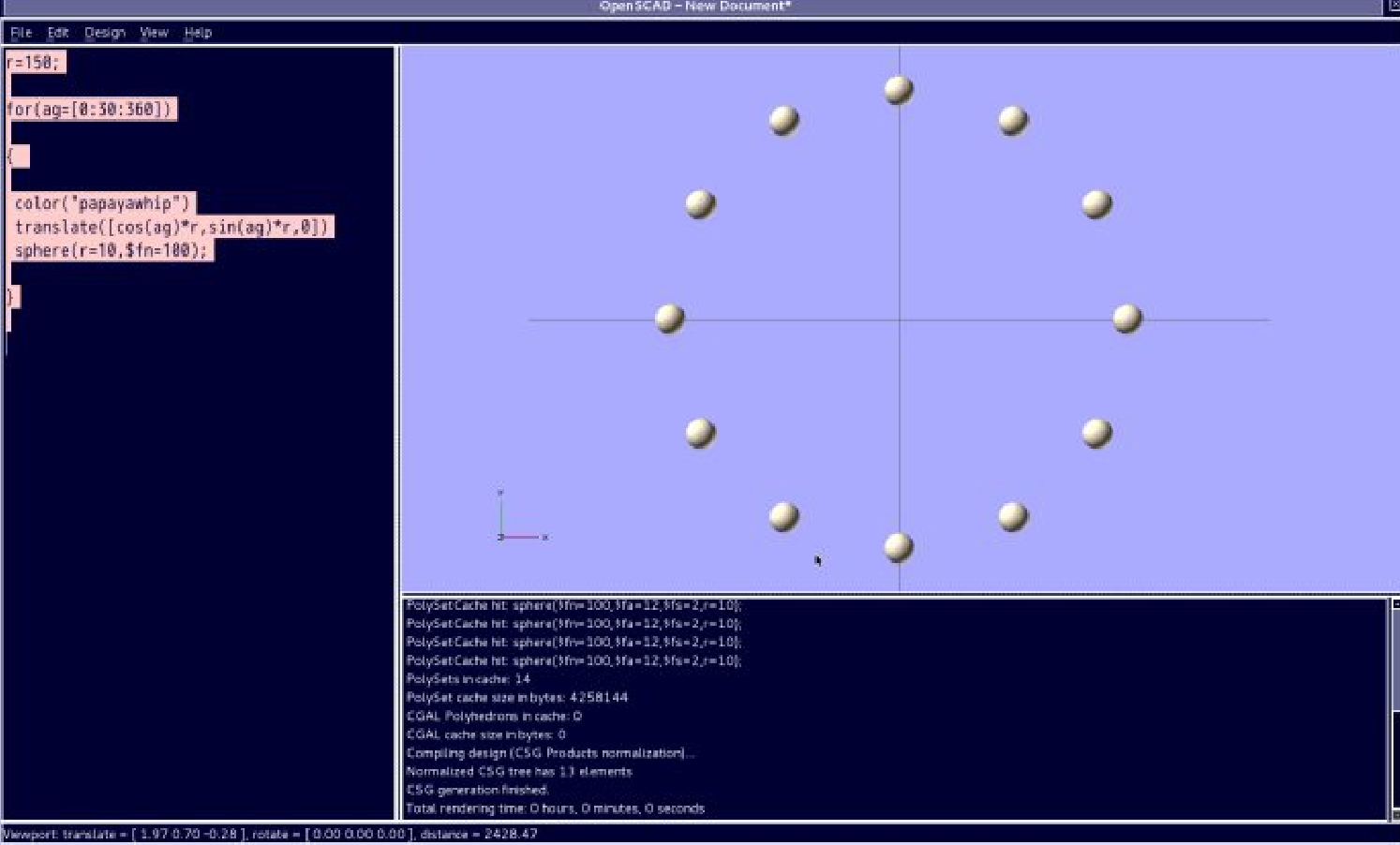
如果机械加工一个球形，机械是 x,y,z, 三个坐标（机械进给系统是三坐标， x ， y ， z 方向），那么其轨迹就是首先加工一个圆形（ x,z 坐标的圆形），然后再以这个圆形的圆心点为中心旋转 ( 以 x, 或者 z 轴为中心旋转），从而可以完成整个球形。
（注意：增加一个嵌套的循环增量 bg, 用于旋转， bg 的密度，决定着旋转的精度；而循环增量 ag 是用于生成一个圆形， ag 的密度，决定着圆弧本身的精度， 不可以仅仅使用一个增量，否则球体无法完成。精度越高，计算的越复杂，计算机反应的速度就越慢，作为轨迹运算，的确很耗费内存。）
还有，当 ag,bg 的增量分别是 5 的时候，计算就超出了范围，引出了一个警告（ WARMING ）。
WARMING ：  Normalized tree has growing past 4000 elements. Aborting normalization.
WARMING: Normalized tree has 4000 elements.
WARMING: openCSG rendering has been disabled!
因为 openCSG 最多支持 4000 个模型，正常情况下所有，我们这个球形轨迹超了，但是如果是用引入数据文件（ dat,txt 等基础文本格式的），然后生成一个模型，可以比较灵活的应用数学的功能，后边我们详细的在学习它吧！）
实例代码：

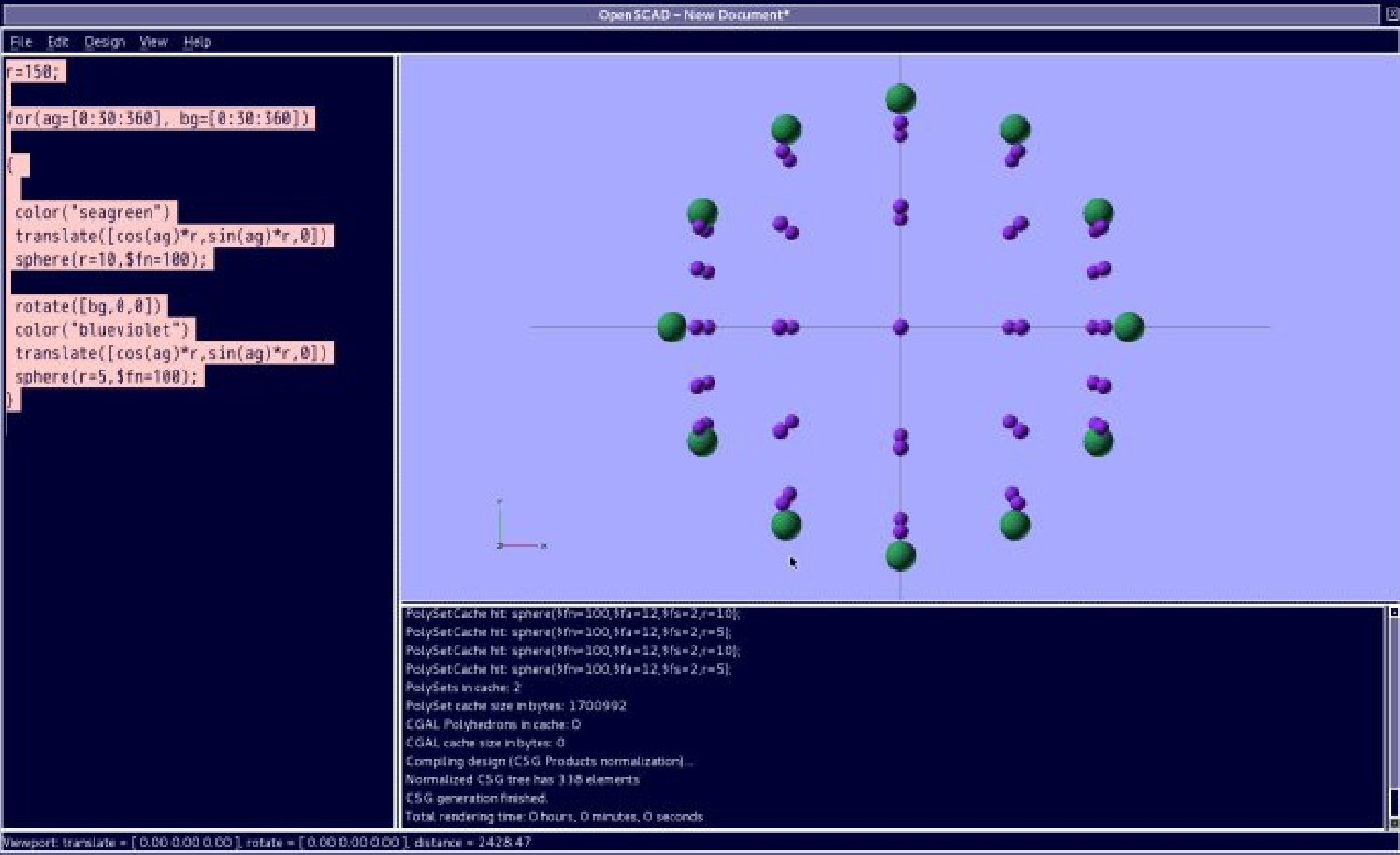
r=150;
for(ag=[0:30:360], bg=[0:30:360])
{
color("seagreen")
translate([cos(ag)*r,sin(ag)*r,0])
sphere(r=10,$fn=100);
rotate([bg,0,0])
color("blueviolet")
translate([cos(ag)*r,sin(ag)*r,0])
sphere(r=5,$fn=100);
}